QU'EST-CE QU'UNE UNITé ASTRONOMIQUE?

Send

En ce qui concerne le cosmos, nous, les humains, aimons exprimer les choses en termes familiers. Lorsque nous examinons les exoplanètes, nous les classons en fonction de leurs similitudes avec les planètes de notre propre système solaire - c'est-à-dire terrestre, géant gazeux, de la taille de la Terre, de la taille de Jupiter, de la taille de Neptune, etc. Et lorsque nous mesurons les distances astronomiques, nous faisons beaucoup de même.

Par exemple, l'un des moyens les plus couramment utilisés pour mesurer les distances dans l'espace est connu sous le nom d'unité astronomique (AU). Basée sur la distance entre la Terre et le Soleil, cette unité permet aux astronomes de caractériser les vastes distances entre les planètes solaires et le Soleil, et entre les planètes extra-solaires et leurs étoiles.

Définition:

Selon la convention astronomique actuelle, une seule unité astronomique équivaut à 149 597 870,7 kilomètres (ou 92 955 807 milles). Cependant, il s'agit de la distance moyenne entre la Terre et le Soleil, car cette distance est sujette à des variations pendant la période orbitale de la Terre. En d'autres termes, la distance entre la Terre et le Soleil varie au cours d'une même année.

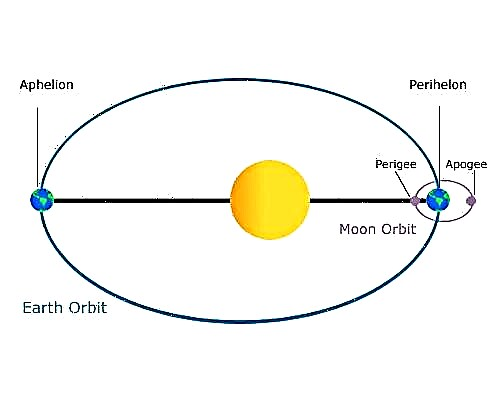
Au cours d'une année, la Terre va d'une distance de 147 095 000 km (91 401 000 mi) du Soleil au périhélie (son point le plus proche) à 152 100 000 km (94 500 000 mi) à l'aphélie (son point le plus éloigné) - ou à une distance de 0,983 UA à 1,016 UA.

Histoire du développement:

Le premier exemple enregistré d'astronomes estimant la distance entre la Terre et le Soleil remonte à l'Antiquité classique. Dans le travail du 3ème siècle avant notre ère, Sur les tailles et les distances du soleil et de la lune - qui est attribuée au mathématicien grec Aristarque de Samos - la distance était estimée entre 18 et 20 fois la distance entre la Terre et la Lune.

Cependant, son Archimède contemporain, dans son travail du 3ème siècle avant notre ère Sandreckoner, a également affirmé qu'Aristarque de Samos avait placé la distance de 10 000 fois le rayon de la Terre. Selon les valeurs de l'un ou l'autre ensemble d'estimations, Aristarque était décalé d'un facteur d'environ 2 (dans le cas du rayon de la Terre) à 20 (la distance entre la Terre et la Lune).

Le plus ancien texte mathématique chinois - le traité du 1er siècle avant notre ère connu sous le nom de Zhoubi Suanjing- contient également une estimation de la distance entre la Terre et le Soleil. Selon le traité anonyme, la distance pourrait être calculée en effectuant des mesures géométriques de la longueur des ombres à midi créées par des objets espacés à des distances spécifiques. Cependant, les calculs étaient basés sur l'idée que la Terre était plate.

Le célèbre mathématicien et astronome du 2e siècle de notre ère, Ptolémée, s'est appuyé sur des calculs trigonométriques pour arriver à une estimation de distance équivalente à 1210 fois le rayon de la Terre. À l'aide des enregistrements des éclipses lunaires, il a estimé le diamètre apparent de la Lune, ainsi que le diamètre apparent du cône d'ombre de la Terre traversé par la Lune lors d'une éclipse lunaire.

En utilisant la parallaxe de la Lune, il a également calculé les tailles apparentes du Soleil et de la Lune et a conclu que le diamètre du Soleil était égal au diamètre de la Lune lorsque celle-ci était à sa plus grande distance de la Terre. De cela, Ptolémée est arrivé à un rapport de distance solaire à lunaire d'environ 19 pour 1, le même chiffre dérivé par Aristarque.

Pendant les mille prochaines années, les estimations de Ptolémée de la distance Terre-Soleil (tout comme la plupart de ses enseignements astronomiques) resteront canoniques parmi les astronomes européens médiévaux et islamiques. Ce n'est qu'au XVIIe siècle que les astronomes ont commencé à reconsidérer et à réviser ses calculs.

Cela a été rendu possible grâce à l'invention du télescope, ainsi qu'aux trois lois de Kepler du mouvement planétaire, qui ont aidé les astronomes à calculer les distances relatives entre les planètes et le Soleil avec une plus grande précision. En mesurant la distance entre la Terre et les autres planètes solaires, les astronomes ont pu effectuer des mesures de parallaxe pour obtenir des valeurs plus précises.

Au 19e siècle, la détermination de la vitesse de la lumière et de la constante de l'aberration de la lumière a donné lieu à la première mesure directe de la distance Terre-Soleil en kilomètres. En 1903, le terme «unité astronomique» a été utilisé pour la première fois. Et tout au long du XXe siècle, les mesures sont devenues de plus en plus précises et sophistiquées, en partie grâce à des observations précises des effets de la théorie de la relativité d'Einstein.

Utilisation moderne:

Dans les années 1960, le développement de mesures radar directes, de la télémétrie et de l'exploration du système solaire avec des sondes spatiales a conduit à des mesures précises de la position des planètes internes et d'autres objets. En 1976, l'Union astronomique internationale (AIU) a adopté une nouvelle définition lors de sa 16e Assemblée générale. Dans le cadre de leur système de constantes astronomiques, la nouvelle définition a déclaré:

«L'unité astronomique de longueur est la longueur (A) pour laquelle la constante gravitationnelle gaussienne (k) prend la valeur 0,01720209895 lorsque les unités de mesure sont les unités astronomiques de longueur, de masse et de temps. Les dimensions de k² sont celles de la constante de gravitation (G), soit L³M^-1T^–². Le terme «distance unitaire» est également utilisé pour la longueur A. »

En réponse au développement de mesures hyper-précises, le Comité international des poids et mesures (CIPM) a décidé de modifier le Système international d'unités (SI) en 1983. Conformément à cela, ils ont redéfini le compteur à mesurer en termes de la vitesse de la lumière dans le vide.

Cependant, en 2012, l'UAI a déterminé que l'égalisation de la relativité rendait la mesure des UA trop complexe et a redéfini l'unité astronomique en termes de mètres. Conformément à cela, un seul UA est égal à 149597870,7 km exactement (92,955807 millions de miles), 499 secondes-lumière, 4,8481368 × 10^-6 d'un parsec, ou 15.812507 × 10^-6 d'une année-lumière.

Aujourd'hui, l'UA est couramment utilisé pour mesurer les distances et créer des modèles numériques pour le système solaire. Il est également utilisé pour mesurer les systèmes extra-solaires, calculer l'étendue des nuages protoplanétaires ou la distance entre les planètes extra-solaires et leur étoile parente. Lors de la mesure des distances interstellaires, les UA sont trop petits pour offrir des mesures pratiques. À ce titre, d'autres unités - telles que le parsec et l'année-lumière - sont utilisées.

L'Univers est un endroit immense, et mesurer même notre petit coin de celui-ci produisant des résultats stupéfiants. Mais comme toujours, nous préférons les exprimer de manière aussi familière et familière.

Nous avons écrit de nombreux articles intéressants sur les distances dans le système solaire ici à Space Magazine. Voici à quelle distance sont les planètes du Soleil?, À quelle distance est Mercure du Soleil?, À quelle distance est Vénus du Soleil?, À quelle distance est la Terre du Soleil?, À quelle distance est Mars du Soleil?, À quelle distance Jupiter du Soleil?, À quelle distance est Saturne du Soleil?, À quelle distance est Uranus du Soleil?, À quelle distance est Neptune du Soleil?, À quelle distance est Pluton du Soleil?

Si vous souhaitez plus d'informations sur l'orbite de la Terre, consultez la page d'exploration du système solaire de la NASA.

Nous avons également enregistré un épisode d'Astronomy Cast dédié à la mesure des distances en astronomie. Écoutez ici, épisode 10: Mesurer la distance dans l'univers.

Sources: